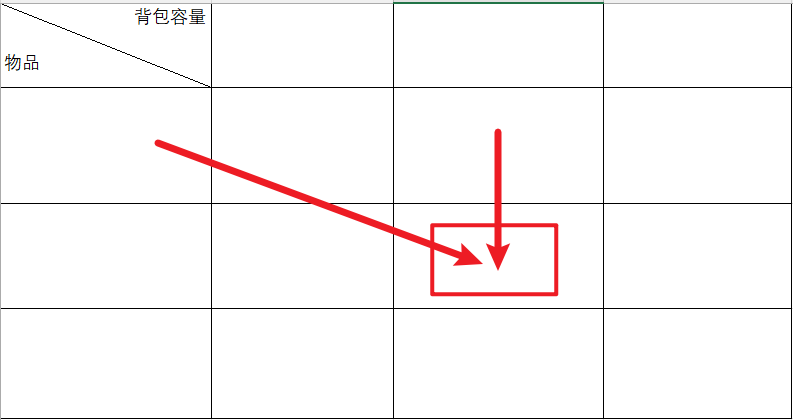
背包问题算法 01背包问题01背包是一种动态规划问题。动态规划的核心就是状态转移方程有一个容量为V的背包，还有n个物体。现在忽略物体实际几何形状，我们认为只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积w和价值v。 问：如何向背包装物体才能使背包中物体的总价值最大？二维数组解法f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[j])i：选用前i种物品j：背包容量为jdp[i][j] 表示从下标为[0，i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。for (int j = 0 ; j < weight[0]; j++) { // 如果把dp数组预先初始化为0了，这一步就可以省略。 dp[0][j] = 0; } // 正序遍历 for (int j = weight[0]; j <= bagWeight; j++) { dp[0][j] = value[0]; }有两个遍历维度：1. 物品和背包容量。 2. 所以要确定遍历顺序。两者都可以，先遍历物品好理解。先遍历物品，然后遍历背包重量：// weight数组的大小 就是物品个数 for(int i = 1; i < weight.size(); i++) { // 遍历物品 for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果不能放下物品i else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); } } 先遍历背包，再遍历物品：// weight数组的大小就是物品个数 for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 for(int i = 1; i < weight.size(); i++) { // 遍历物品 if (j < weight[i]) dp[i][j] = dp[i - 1][j]; else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); } }为什么两种顺序都可以？要理解递归的本质和递推的方向。那么先遍历物品，再遍历背包的过程和先遍历背包，再遍历物品，dp[i][j]所需要的数据就是左上角，根本不影响dp[i][j]公式的推导。一维dp数组解决01背包问题dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);一维dp数组如何初始化dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。一维dp数组遍历顺序for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }在01背包中二维dp数组的两个for遍历的先后循序是可以颠倒，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。和二维dp的写法中，遍历背包的顺序是不一样的！一维dp遍历的时候，背包容量是从大到小：倒序遍历是为了保证物品i只被放入一次！为什么一维dp数组必须倒序遍历：如图，红线为数据更新来源，蓝线数据更新顺序：当前状态源于左上角和同背包容量方向如果先遍历物品再遍历背包且正序遍历，就会使一些同背包容量方向的数据被覆盖掉。如果先遍历背包再遍历物品，完全背包问题完全背包依然是一个动态规划问题有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。01背包和完全背包唯一不同就是体现在遍历顺序上，所以针对遍历顺序进行分析。// 先遍历物品，再遍历背包 int[] dp = new int[bagWeight + 1]; for (int i = 0; i < weight.length; i++){ for (int j = 1; j <= bagWeight; j++){ if (j - weight[i] >= 0){ dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); } } }为什么遍历物品在外层循环，遍历背包容量在内层循环？在01背包中二维dp数组的两个for遍历的先后循序是可以颠倒，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序无所谓：因为物品可以重复装。也就是说dp[j]是根据下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以。完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值。为什么是正序遍历而不是倒序遍历了？因为在完全背包中，由于物品可以重复装填，那么就需要相同物品在不同背包容量时重复利用前面的数据。先遍历背包再遍历物品：// 先遍历背包，再遍历物品 for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 for(int i = 0; i < weight.size(); i++) { // 遍历物品 if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }先遍历物品，再遍历背包：// 先遍历物品，再遍历背包 int[] dp = new int[bagWeight + 1]; for (int i = 0; i < weight.length; i++){ for (int j = 1; j <= bagWeight; j++){ if (j - weight[i] >= 0){ dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); } } }连续背包问题连续背包问题是指有一个容量为V的背包和n个物品，每个物品有一个体积v [i]和一个价值w [i]，现在要将这些物品放入背包中，使得背包中物品的总价值最大。 与0/1背包问题不同的是，每个物品可以被放入多次，即是连续的。解题思路：单位价值优先使用贪心算法① 按价值密度(w/v)进行非递增排序② 按照排序先后，往里装。单个物品装完时换下一个，直到背包填满为止